唐艳敏

　　(河南师范大学 河南 新乡 453007)

　　数学归纳法在中学数学中的应用

　　唐艳敏

　　(河南师范大学 河南 新乡 453007)

　　数学归纳法作为我们学习数学的一种十分重要的思想方法常被应用于证明某个给定的数学命题在整个自然数范围内成立,它主要是在解决数学问题的过程中利用对事例有限次的假设，证明来替代对事例进行的无限次论证,进而使命题能够得到严格的证明。本文阐述由数学归纳法验证命题成立的一般步骤,并用具体实例来详细的阐诉数学中的应用,并对其作用、重要性及应用所需注意事项进行总结。

1 用数学归纳法证明题目的一般步骤

数学归纳法对于在实际的课堂中指导中学生更加容易的学习与研究数学十分有用。它首先通过直观的导入方式,使同学们在感官方面对它有一个简单的认识,再通过后期对他们的指导培养,使他们逐渐形成一个有条理的、完善的数学归纳法知识结构体系。在课堂上,通过具体实例论证使其获得与数学归纳法相关的感性材料,从而就有了对其初步的感性认识。在这样的基础上,我们就能够把数学归纳法的相关概念和具体证题步骤更加直观的呈现在同学们面前。

　　1.1 第一数学归纳法

　　如果某一个命题Fn是和自然数n有关系的,若(1)命题Fn在n=1时成立；(2)假定命题Fn在n=k(k∈N )时成立,则可以验证出命题Fn对于k+1也是成立的,那么命题Fn对于所有自然数n都是成立的[1]。

　　1.2 第二数学归纳法

　　如果某一个命题Fn是和自然数n有关系的,若(1) 命题Fn在n=1时成立；(2)假定当1≤n≤k时,Fn都是成立的,则(3)当n=k+1时,Fn对于k+1也是成立的,那么有,对一切的自然数n,都有Fn成立[2]。

　　其实,我们从上面给出的概念很容易看出来这两种归纳法其实是一样的,它们只是对数学归纳法的不同表示形式,并且这两种方法基本上是相通的。由两种方法证题步骤可知,后者显然能够得到前者；反过来,由前者也能够得出后者。由于,在n=k时,Fn是成立的,且当n=k+1时,命题Fn对于k+1也是成立的,则明显有1≤n≤k时,Fn也都是成立的。由第一归纳法和第二归纳法的共同特征我们可以概括出数学归纳法的基本形式；(1)检验当n取第一个值的时候命题成立;(2)假定当n=k时命题正确,可以验证当n=k+1时,命题也正确;(3)由前两步的结果我们可以判断出命题取任意的自然数时都是成立的。

2 数学归纳法的应用

在数学的学习过程中我们常常会用到数学归纳法,尽管它在某种程度上有一定的局限性,但它在中学数学中依旧发挥着不可替代的作用。但是要想真正地掌握、准确的应用数学归纳法必须抓住数学归纳法的核心要义,并能够深刻理解它的内涵,然后能够灵活多变的应用数学的思维方法,做到具体情况具体分析。

3 用于解决数列问题

数列问题是一类与自然数密切相关的问题。因而,在解决数列问题时,我们自然而然就会联想到用数学归纳法的相关知识来处理此类问题。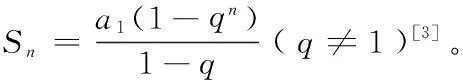

　　

　　证明：(1)当n=1时,S1=a1,即等式成立;

　　

　　所以当n=k+1时命题成立；

　　

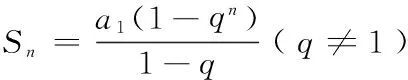
　　HTH〗4 用于证明恒等式问题

　　对于代数恒等式的证明也可以用数学归纳法来解决,但大多数学生在用这个方法解决问题的时候却感觉到无从下手,而这主要是他们没有能够找到明确的证明目标。在解决此类恒等式的问题时,首先应该学会分析等式两边的特点,然后要在第二步中将所需要证明等式转化为能够与题目中归纳假设的结构相类似的证明形式,同时要注意在第二步中的式子的转换过程应该尽量详细,不可以简单一笔带过[4]。

　　例2 求证:(n+1)(n+2)(n+3)…(n+n)=2n·1·3·5…(2n-1)(n∈N* )

　　证明: (1)当n=1的时候,等式左=1+1=2,等式右=1×2=2,左=右,所以原式能够成立；

　　(2)假设n=k(k∈N*)时,等式成立,也即有等式

　　(k+1)(k+2)…(k+k)=2k·1·3·5…(2k-1)

　　那么n=k+1时,

　　(k+2(k+3…(k+k)(2k+1)(2k+2)=2(k+1)(k+2)(k+3)…(k+k)(2k+1)

　　=2k+1·1·3·5…(2k-1)[2(k+1)-1]

　　所以当n=k+1时,等式成立。

　　综上可以知道,对于任何n∈N* 都有

　　(n+1)(n+2)(n+3)…(n+n)=2n·1·3·5…(2n-1)(n∈N* )

　　成立．

5 用于证明不等式问题

在证明不等式的相关问题时候也可以使用数学归纳法来解决,首先应该比较n=k和n=k+1这两个不等式之间的区别,然后再决定n=k时不等式应该做怎么样的变形,一般的情况下,我们只是能够得出等式的一边,最后可以利用分析法、比较法、放缩法、综合法以及不等式之间传递性等来根据由n=k成立时的式子再推出n=k+1时不等式所成立时的结果,从而完成证明。不等式的证明与恒等式的证明相比较有很多相似的地方,其最重要的仍然在于第二步[5]。不过不等式证明的难度会比较大一些,有的在第一步也不是那么的容易。

　　

　　

　　

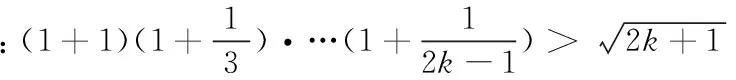
　　当n=k+1时

　　∴n=k+1时成立

6 用于证明整除问题

用数学归纳法解决整除的相关问题,能够在很大程度上降低我们在解题时的难度。第一步可以根据题目中所需要被证明的式子进行添项、去项来变形,从而能够凑出使原来的假设可以成立时的式子；第二步再来验证余下的式子也可以被某一个式子整除,这是我们用这种方法证明整数的整除类问题的一个重要技巧[6]。

　　例4 对于n∈N*,求证：(x+1)n+1+(x+2)2n-1,可被(x2+3x+3)整除。

　　证明：(1)当n=1时,左边=(x+1)2+(x+2)1=x2+3x+3成立

　　(2)假设n=k时成立,即：(x+1)k+1+(x+2)2k-1=(x2+3x+3)·f(x)

　　当n=k+1时

　　(x+1)k+2+(x+2)2k+1

　　=(x+1)(x+1)k+1+(x2+4x+4)(x+2)2k-1

　　=(x+1)(x+1)k+1+(x+1)(x+2)2k-1+(x2+3x+3)·(x+2)2k-1

　　=(x+1)·(x2+3x+3)·f(x)+(x2+3x+3)(x+2)2k-1

　　=(x2+3x+3)·[(x+1)·f(x)+(x+2)2k-1]

　　所以n=k+1时成立。

　　综合(1)(2)可以知道,对一切n∈N*,都有(x+1)n+1+(x+2)2n-1可以被(x2+3x+3)整除。

7 用于证明几何问题

几何在中学数学中是一个相当重要的研究方向,同时几何问题相对来说又是比较抽象的,所以常常采用数学归纳法来进行几何问题的相关证明,这样就会降低解决此类问题的难度,简化它的繁琐过程。但是,在处理这种类型的问题时需要注意:解决此类问题之前首先应该找出规律,然后再获取公式,之后才能够利用这种方法来论证所要得到的结果[7]。

　　例5 在一个平面上一共有n条直线(n∈N*,n≥2),在这n条直线中，任何两条直线之间都是不平行的,并且任何三条直线之间都是没有公共点的[8]。

　　

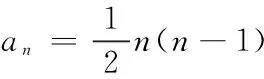
　　(2)在这n条直线中能够相互构成射线或线段的直线有bn=n2条；

　　证明:(1)① 根据题意可以知道,当n=2时,a2=1,此时原式成立；

　　

　　

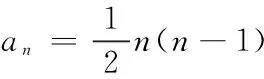
　　(2)① 当n=2时,b2=4,原式成立；

　　② 假设n=k时成立,即bk=k2,

　　当n=k+1时,可以知道第k+1条直线上有k个交点,也就是说将第k+1条直线分成k+1个部分,k个交点还在原k条线上,即每一点都将所在射线或线段分成两部分。

　　所以ak+1=ak+(k+1)+k=k2+2k+1=(k+1)2,即当n=k+1时原式成立。

　　综上得知,对于一切n∈N*,n>1时都有bn=n2。

8 总结

本文介绍了数学归纳法在解决问题时的一般步骤,以及在中学数学中的数列、恒等式、不等式、整除以及几何问题中的具体应用。因此针对大多数与自然数相关的性质,我们都能够用数学归纳法来进行证明。但是在运用这种方法的时候我们也要注意一些问题: ①利用数学归纳法能够解决一些与自然数相关的问题,但是并非在我们遇到的所有相关的此类数学问题时都能够利用这种方法来进行解决[10]；②利用数学归纳法在解决问题的时候,首次所选取的值必须要满足问题中条件所给定的第一个数(这个数并不一定要求为1)；③虽然数学归纳法是用来解决与正整数相关的数学问题的一种比较有用的方法,可是利用这种方法我们通常只能够验证命题是否正确,却不能够根据它来寻找到更多新命题；

　　对于数学归纳法广泛应用和优越的性质我们还要继续的加以探索和研究。从而帮助学生更加清晰地理解数学归纳法,以及有效地运用。

　　[1] 孟涣晨.数学归纳法及其应用[J].科教文汇,2009,16: 119.

　　[2] 谢发超.数学作文的命题研究[M].重庆：西宁师范大学出版社,2006:72.

　　[3] 甘志国,邓晓峰.用函数观点求解数列问题[J].中学数学研究,2011,9;38-40.

　　[4] 王曙东,数学归纳法的几大应用[J].中学数学,2012,9:93.

　　[5] 刘金娜.对数学归纳法的认识[J].考试周刊,2011,28:87-88.

　　[6]WilliamL.Sanders,S.PaulWright,SandraP.Horn.TeacherandClassroomContextEffectsonStudentAchievement:ImplicationsforTeacherEvaluation[J].JournalofPersonalEvaluationinEducation. 1997(1).

　　[7] 张先达.数学归纳法在中学的应用[J].经济研究导刊.数学通报,2014,8：304-305.

　　[8] 高考一轮总复习编写组.2014走向高考[M].中国和平出版社.2012,7:176.

　　[9]Carr,S.C.Assessinglearningprocesses:Usefulinformationforteachersandstudents.InterventioninSchoolandClinic.2002.

　　[10] 钱佩玲.中学数学思想方法.北京师范大学出版社,2000,6:204-205.

　　G633

　　A

　　1672-5832(2016)03-0173-02