

摘要:本文采用多变量SVAR模型对我国和“一带一路”沿线19个样本国家进行经济冲击性检验,并进一步分析我国和沿线国家之间货币合作的可行性,进而得出主要结论:我国在和“一带一路”沿线国家货币合作中尚未充分发挥核心主导国作用;我国同“一带一路”沿线国家之间存在比较广泛的非对称性,沿线国家整体的货币合作条件尚不具备,但沿线国家内部存在对称性相对较高的子集团;沿线国家供给冲击比货币冲击、需求冲击对称性更高;“一路”沿线国家经济冲击的对称性高于“一带”沿线国家和中东欧国家,适合率先开展货币合作,我国同“一路”沿线国家具备优先开展货币合作的优势和基础。基于以上研究结论,本文给出了未来推进货币合作和人民币国际化的相关对策建议。
关键词:人民币国际化;供给冲击;需求冲击;货币冲击;SVAR模型
中图分类号:F820? ? 文献标志码:A? ? 文章编号:1001-862X(2020)05-0037-006
自2013年我国提出并实施“一带一路”倡议以来,人民币国际化水平得到了较大的提升。“一带一路”倡议的实施有利于增强人民币国际化的经济、金融基础,也有利于扩大人民币在沿线国家的使用范围,为人民币国际化提供了新的机遇。然而,迄今为止,人民币仍未获得与我国国际经济、贸易地位相匹配的国际地位,同美元、欧元等国际货币相比,人民币在国际支付结算和官方外汇储备中所占的份额仍然较低。同时,人民币国际化的进程在近年来也出现了较大的波动。[1]在目前国际经济、贸易形势不断变化的情况下,如何通过“一带一路”的建设,进一步推进人民币国际化是我们亟须思考和亟待解决的问题。
一、文献综述
货币合作的相关研究以Mundell(1961)提出的最优货币区(OCA)理论为基础,早期的OCA理论经过McKinnon、Kenen和Ingram等经济学家的发展和补充,形成了一套关于货币合作“事前”评价标准的传统OCA理论。传统的OCA理论着重于定性分析,依据不同的评价标准得出的结论也不尽一致。20世纪90年代以来,随着计量经济学的发展,Bayoumi & Eichengreen(1996、1997)基于传统OCA理论的各项评价标准,提出了OCA指数法,来综合测度货币合作的成本。传统OCA理论忽视了评价标准和货币合作之间的内生性,Frankel & Rose (1998)首先提出了内生性OCA理论,认为区域货币合作会提高区域贸易一体化水平,降低区域内非对称冲击程度,从而达到最优货币区的构建标准。在此基础上,Blanchard & Quan(1989)最早在有关经济长期冲击效应的相关研究中,引入两变量SVAR模型(简称为B-Q模型)。Bayoumi & Eichengreen C(1994)利用两变量SVAR模型,对东亚各国潜在的经济冲击效应进行了检测,判断东亚各国是否满足货币联盟构建标准。基于OCA指数法和SVAR模型,国内外学者针对欧元区、拉美、东亚等区域的货币合作展开了较为广泛的研究。
基于区域货币合作视角考察人民币国际化问题的相关研究成果主要集中于内地和港澳台、中日韩、东亚及东盟地区的应用分析。在研究视角上,主要包括:通过测算货币合作成本和经济一体化内生性检验判断人民币国际化的可行性和人民币国际化的实现路径。目前,在“一带一路”背景下从货币合作的视角研究人民币国际化推进问题的实证研究还比较缺乏,学者们主要是基于欧元区、东亚、拉美等区域货币合作的研究方法,通过选取不同的沿线样本国家、建立不同的OCA指标体系去测度丝绸之路经济带、中亚五国、沿线国家整体的货币合作成本,判断人民币区域化和国际化的可行性,并进一步探讨如何规划人民币国际化路径。也有学者开始对我国和沿线国家之间的经济一体化内生性进行检验,比较分析美元和人民币对沿线国家的锚货币效应,但选择的样本国家和变量比较有限。
二、研究设计
根据前文研究理论和本文的研究目的,考虑数据的可得性,本文首先选取了“一带一路”沿线19个样本国家,在样本数据平稳性检验的基础上,通过施加长期约束条件,建立多变量SVAR模型。最后对模型平稳性进行检验,并对我国和沿线样本国家之间经济冲击系数做出估计。
(一)样本国家的选取与数据说明
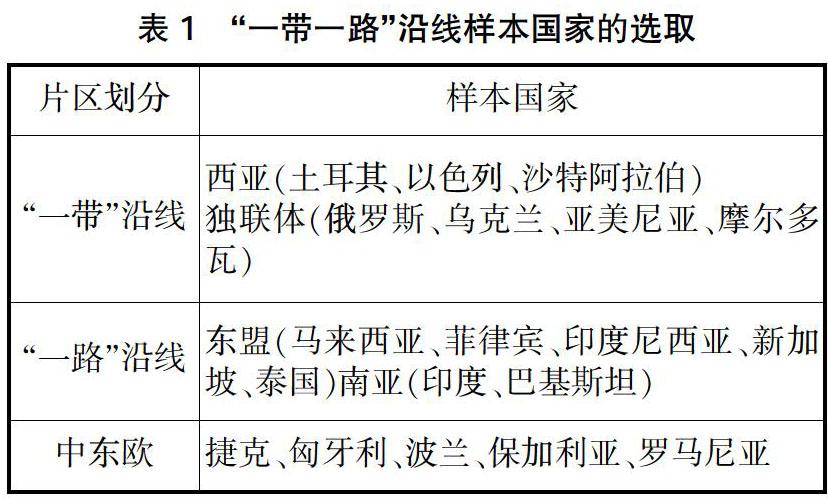
基于“一带一路”沿线国家不同区域的异质性特征,本文还将“一带一路”沿线国家划分为三个片区(分别为“一带”沿线、“一路”沿线和中东欧国家),样本国家的选取情况见表1。本文选择的样本期为1997—2018年。“一带一路”沿线其他国家由于数据缺失或者样本时间段过短等原因没有纳入研究范围。
本文选择以2010年不变美元计算的GDP、消费者物价指数CPI(其中2010年指数值设为100)、实际有效汇率指数EFFR(其中2010年指数值设为100)分别作为沿线国家总产出水平、价格水平和实际有效汇率的研究指标,相关数据来源于世界银行WDI数据库、IMF的《国际金融统计年鉴》、国际清算银行BIS数据库。所有数据均为年度数据。本文所有数据处理及计算结果采用Eviews8.0和Stata14.0操作完成。
(二)SVAR模型的建立及变量的选取
SVAR模型是检验经济冲击对称性的重要方法,Sims(1986)将VAR模型发展为SVAR模型,弥补了VAR模型缺乏经济理论解释的缺陷,并能较好地反映变量之间的当期关系。
本文在Bayoumi(1989)& Eichengreen(1994)的研究方法基础上,通过施加长期约束性条件,将结構性经济冲击分解为供给冲击、货币冲击和需求冲击,构建三变量SVAR模型。本文参考Ramos & Surinach(2004)中货币冲击变量的选择,以实际有效汇率作为货币冲击的代表指标。
首先设定一个三元p阶的SVAR模型的一般表达式:
C0yt=Γ1yt-1+Γ2yt-2+…+Γpyt-p+εt(1)
其中:
C0= 1? ?-c12? -c13-c21? ?1? ?-c23-c31? -c32? ?1Γi=γ(i)11? γ(i)12? γ(i)13γ(i)21? γ(i)22? γ(i)23γ(i)31? γ(i)32? γ(i)33(i=1,2,…,P)
εt=ε1tε2tε3t
(1)式也可以写成滞后算子的形式(L为滞后算子):
yt=y1ty2ty3t=A11(L)? A12(L)? A13(L)A21(L)? A22(L)? A23(L)A31(L)? A32(L)? A33(L)ε1tε2tε3t=A(L)εt
(2)
其中,y1t、y2t、y3t分别代表宏观经济产出水平、实际有效汇率和价格水平,均为平稳随机过程;表示结构性经济冲击,ε1t、ε2t、ε3t均为白噪声序列,分别表示供给冲击、货币冲击和需求冲击,序列之间互不相关;A(L)为滞后算子L的多项式,代表内生变量对经济冲击的脉冲响应。
为了对SVAR模型进行有效识别,需要根据相关经济理论对结构式施加长期约束性条件。根据内生变量的个数,至少需要施加k(k-1)/2个(k为内生变量的个数)限制性条件。
根据弗里德曼的货币中性理论,在长期内,货币冲击会对价格水平产生影响,但不改变总产出水平,即货币冲击对产出水平没有长期影响。在AD-AS模型中,需求冲击在短期里会改变总产量和价格水平,但对长期潜在产出水平没有影响。因此,需求冲击对价格水平有长期影响,对产出水平没有长期影响,对剔除价格变动因素后的实际有效汇率也不产生长期影响。
因此,本文对结构式施加三个约束性条件来识别SVAR模型,即:
(1)货币冲击和需求冲击对产出水平没有长期影响;
(2)供给冲击和货币冲击对实际有效汇率有长期影响,需求冲击对实际有效汇率没有长期影响;
(3)供给冲击、需求冲击和货币冲击对价格水平都有长期影响。
因此,(2)式中A12(L)=A13(L)=A23(L)=0,系数矩阵A(L)为下三角矩阵。SVAR模型可以重写成如下形式:
yt=y1ty2ty3t=A11(L)? ? ?0? ? ? ? 0A21(L)? A22(L)? ? 0A31(L)? A32(L)? A33(L)ε1tε2tε3t
考虑到SVAR模型中的结构性残差不能直接被估计,因此需要先写出上述三变量简约式VAR模型表达式:
yt=B(L)Xt-1+μt(3)
根据(2)(3)表达式可知,SVAR模型和简约式VAR模型残差的关系为:μt=A0 εt。其中,μt为简化式残差,εt为结构式残差。简化式残差μt为复合冲击,是εt的线性组合。
首先需要对无约束VAR模型进行最小二乘估计,求出简化式残差的估计值;再对无约束VAR模型施加长期约束性条件,求出A0矩阵的估计值,最后根据εt=A-10μt求出结构式残差的估计值。
(三)平稳性检验
为保证SVAR模型建立的稳定性,首先对各国GDP、EFFR及CPI原始数据进行单位根检验。为减少时间序列数据可能产生的异方差,首先对原始数据取对数,分别以lnGDP、lnEFFR和lnCPI表示。以d1lnGDP、d1lnEFFR、d1lnCPI表示原序列数据取对数后的一阶差分,对取对数后的序列数据和一阶差分序列数据分别进行ADF单位根检验,检验结果显示所有样本国家的一阶差分数据都能在5%的水平通过单位根检验,为一阶单整序列数据,满足模型的建立条件。ADF单位根检验结果见附录(略)。
在单位根检验的基础上,建立样本国家简化式VAR模型(即无约束VAR模型),简化式VAR模型的内生变量为经济增长率、实际有效汇率的波动率及通货膨胀率,分别以上述平稳的一阶差分序列数据进行表示。[2]在估计各国简化式VAR模型时,综合AIC、SC最小化信息准则的原则选择VAR模型的最优滞后阶数,当AIC信息准则与SC信息准则的最小值对应不同阶数的p值时,根据似然比检验统计量LR数值综合确定。综合所有样本国家的分析结果来看,土耳其滞后2阶,乌克兰、亚美尼亚、泰国、波兰滞后3阶,其他国家滞后4阶。为了分析比较的一致性,所有样本国家选择滞后2阶,记为VAR(2)。
对各样本国VAR(2)模型估计后,对模型的稳定性进行检验。如果AR特征方程的特征根小于1,即所有的特征根在单位圆以内,VAR(2)模型是稳定的。通过检验,所有样本国家的VAR(2)模型的特征根都在单位圆以内,模型通过了平稳性检验。各样本国家AR特征图见附录(略)。
(四)SVAR模型的估计
在简化式VAR(2)模型的基础上,对VAR(2)模型施加上文的长期约束条件。首先设定一个3*3阶长期响应矩阵ψ=NA? 0? ?0NA NA? 0NA NA NA,根据上文所述的约束条件,响应矩阵中ψ12=ψ13=ψ23=0。在各国SVAR模型的估计值中,模型为恰好识别。Eviews中SAVR模型估计结果采用Ae=Bu的形式,其中A为单位矩阵,e为简化式VAR(2)模型的残差序列矩阵,根据B矩阵的估计结果求出其逆矩阵,即为上文所述A0的逆矩陣A-10。利用A-10和简化式VAR(2)模型的残差序列可以识别出各国结构式冲击矩阵εt,其中可分解出供给冲击、货币冲击和需求冲击。再对各样本国家的供给冲击、货币冲击和需求冲击序列做相关性分析。
三、实证检验与结果分析
根据SVAR模型冲击系数的估计结果,本文对我国和沿线样本国家经济冲击对称性进行实证分析,并在此基础上利用脉冲响应函数进一步检验了我国和沿线样本国家之间经济冲击规模和冲击调整增速度,最后以脉冲响应函数图考察实际有效汇率对结构性经济冲击的响应模式。
(一)经济冲击的对称性检验
大部分沿线国家之间的供给冲击表现为正的相关性。我国同“一带”沿线国家中的沙特、乌克兰、亚美尼亚和摩尔多瓦呈现出较低的相关性,和“一带”沿线大部分国家之间经济融合度不高。西亚国家之间相关性较高,以色列和土耳其的相关系数高达0.946,西亚国家之间已经初步具备了货币合作的基础。独联体国家之间供给冲击相关系数差异较大,并不适合进行货币合作。我国同“一路”沿线国家中的新加坡、印度、巴基斯坦之间呈现正的相关性,东盟国家中除了泰国和印尼,其他国家之间都呈现出比较稳定的正相关性,相关系数约在0.2~0.7之间。南亚和中国及其他东盟国家之间也保持着较好的对称性。中东欧国家之间供给冲击的对称性有一定的差异,未来开展区域货币合作的经济基础也有待加强。
沿线国家之间货币冲击的相关性要弱于供给冲击,我国同多数沿线国家存在广泛的货币冲击的非对称性。西亚国家之间基本都保持着货币冲击的非对称性,这说明西亚不同国家之间金融发展水平存在比较显著的异质性。独联体内部货币冲击的对称性较好。东盟国家之间基本呈现出比较稳定的对称性,相关系数在0.2~0.6之间,南亚的印度和巴基斯坦之间货币冲击呈现出非对称性,和其他东盟国家之间相关系数也有正有负。中东欧国家之间货币冲击呈现出较好的对称性,但多数国家和我国呈现出非对称性,这说明中东欧不同国家之间金融发展水平比较接近,有着比较相似的金融政策治理效果。
相较于供给冲击的相关性,需求冲击整体上也要弱一些。在“一带”沿线国家,我国仅和沙特呈现出需求冲击的正相关性,和其他国家之间都是非常显著的不对称性,未来货币合作需要付出较高的政策协调成本。西亚国家之间需求冲击的对称性比较高,尤其是土耳其和以色列,需求冲击的相关系数高达0.782。独联体国家之间需求冲击的对称性不太稳定。我国和“一路”沿线国家需求冲击的相关性更高一些,东盟国家中除了印尼,其他国家之间都呈现出正相关性。南亚和多数东盟国家也是呈现出需求冲击的非对称性。中东欧国家之间需求冲击差异比较明显,捷克、匈牙利和其他中东欧国家呈现出冲击的对称性。
(二)经济冲击规模和冲击调整速度的比较分析
本文在SVAR模型估计的基础上,利用脉冲响应函数结构式冲击的随机干扰项对内生变量未来取值的影响加以判断,以此来考察沿线各国经济冲击规模和冲击调整速度。
本文以各内生变量对一个标准差的结构式冲击在若干滞后期后脉冲响应绝对值的加和平均数作为经济冲击规模的测算结果,以脉冲响应函数响应值短期累计滞后值之和占长期累计滞后值之和的比值作为经济冲击的调整速度。考虑到供给冲击的长期效应及货币冲击和需求冲击的短期效应,本文以一个标准差的供给冲击对经济增长率滞后20期的脉冲响应绝对值的加和平均数作为沿线各国供给冲击的规模;以一个标准差的货币冲击对实际有效汇率波动率滞后2期的脉冲响应绝对值的加和平均数作为沿线各国货币冲击的规模;以一个标准差的需求冲击对通货膨胀率滞后2期的脉冲响应绝对值的加和平均数作为沿线各国需求冲击的规模;以各内生变量滞后4期的脉冲响应累计值之和占滞后20期的脉冲响应累计值之和的比值作为沿线各国的冲击调整速度。
从经济冲击规模和冲击调整速度的计算结果来看,我国供给冲击规模超过了“一路”沿线国家和中东欧国家的均值水平,供给冲击的调整速度也是所有国家中最慢的;货币冲击规模较小,调整速度较快;需求冲击规模也超过了“一路”沿线国家均值水平,但调整速度较快。这说明,我国在同沿线各国的货币合作方面尚没有充分发挥核心主导国家的推动作用。整体来看,“一路”沿线国家供给冲击、货币冲击和需求冲击的规模都是最小的,其次是中东欧国家,冲击规模最大的是“一带”沿线国家。在冲击的调整速度上,中东欧国家供给冲击的调整速度是最快的,但需求冲击和货币冲击的调整速度最慢;“一带”沿线国家需求冲击和货币冲击的调整速度是最快的,“一路”沿线国家供给冲击的调整速度最慢。
(三)脉冲响应函数分析
本文采用SVAR模型中脉冲响应函数图形考察实际有效汇率对结构性经济冲击的响应模式,一个标准差的供给冲击和货币冲击对各国滞后20期的实际有效汇率的冲击影响作为分析的基础。
从实际有效汇率的波动率对供给冲击的脉冲响应过程上看,中国、沙特阿拉伯、亚美尼亚、摩尔多瓦、马来西亚、泰国、捷克、匈牙利基本都是在第1期产生了一个较大的负响应,然后逐漸震荡上升,大约在第4期达到正响应的最大值,在第16—18期冲击趋于收敛,其中泰国和捷克的震荡周期更短,大约在第8—10期后脉冲响应值就趋向于0。其他国家基本是在第1期产生一个正响应,然后逐渐震荡下降,大约在第4期达到负响应的最大值,在第10—14期趋于收敛。就整体来看,多数国家都是在第4—6期达到供给冲击脉冲响应的正效应或负效应的最大值。“一带一路”沿线国家中,我国同东盟五国及中东欧国家中的捷克和匈牙利有着比较相似的震荡走势,基本都是经过前2期的波动震荡,在2—4期达到正响应的最大值,在12—14期趋向收敛平稳。
相比于供给冲击,“一带一路”沿线各国实际有效汇率的波动率对货币冲击的脉冲响应相似度更高,大部分国家都是在第1期产生了一个较大的正向脉冲响应值,然后震荡下降,大约在第4—6期达到负响应的最大值,但不同国家震荡幅度不同,然后在第10—14期趋于收敛平稳。“一带一路”沿线国家中,我国同土耳其、以色列、独联体国家、东盟五国、印度、捷克、匈牙利、保加利亚、罗马尼亚在震荡走势上比较相似,都是在第1期取了一个较大的正响应值以后,第2期脉冲响应值迅速下降,经过6—8期的轻微震荡,脉冲响应值趋于0。





