张文嘉
　　
　　几何中，余弦定理有很多证明方法，只要不触犯“禁止逻循环辑论证”规则，即为有效证明方法。这里是一种利用数的乘法功能与独立变量的组合数学建模思想，将“数”“形”结起来，证明余弦定理的方法。
　　一、利用数的乘法功能
　　做一件事，完成它可以有n类办法，在第一类办法中有m1种不同的方法，在第二类办法中有m2种不同的方法，……，在第n类办法中有mn种不同的方法，那么完成这件事共有N=m1+m2+m3+…+mn种不同方法。
　　特别的，当m1=m2=m3=…=mn时。我们用字母t代替，即
　　m1=m2=m3=…=mn=t
　　则N=m1+m2+m3+…+mn=t×n
　　为了快速统计，逆用该公式，我们按一组t个进行分组，组数为n，整体统计结果N，我们可以用t×n代替评价。
　　我们如果按一组n个进行分组，组数为t，整体统计结果认为N，我们可以用n×t代替评价。
　　不难发现：t×n=n×t=N，n，t位置可以交换（我们称之谓服从交换律，地位平等）。乘法口诀本质上是建立“分组标准n，组数t”与加法结果N之间的因果关系。因此，乘法有乘法具有任意拆分后的整体量评价功能。
　　推而广之，我们忽略n，t的单位，抽象出无量纲的数的独立变量。n，t可以作为两个无量纲的数的独立变量，t×n可以评价任何事物特征的工具之一。
　　二、利用独立变量的组合数学建模思想提出合理假设
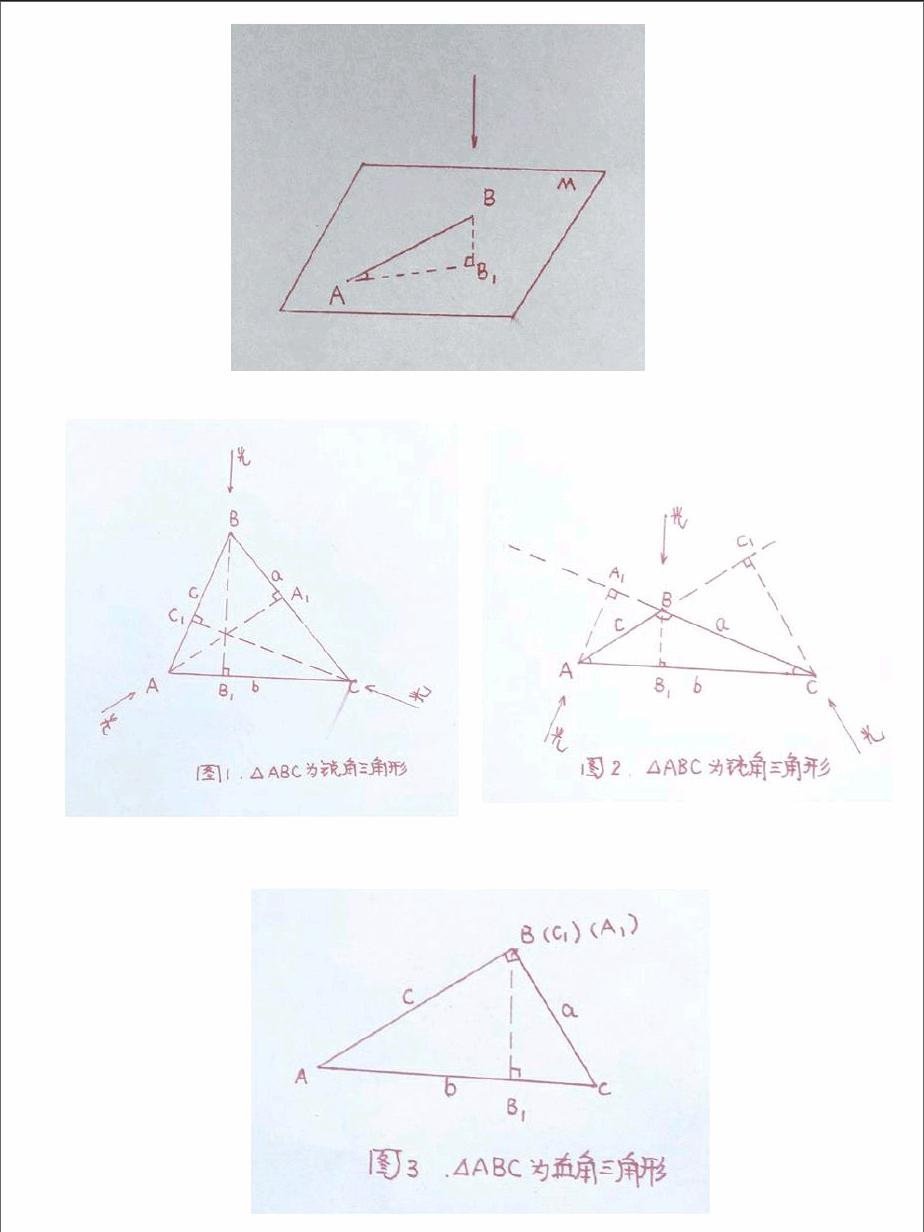
　　假设任何线段AB在垂直于某平面M（点A在平面内）的光的照射下，在其平面的M内影长|AB1|只与线段AB的长度|AB|、线段AB与平面M夹角n两个独立变量有关。设F（n）为 夹角n造影能力。
　　线段AB的长度|AB|、夹角n造影能力F（n）是影响“影长|AB1|的两个独立变量”。
　　于是，可以假设影长|AB1|=|AB|×F（n）+X X为常数。
　　根据生活经验，AB平行于光，在其平面的M内影长|AB1|=0，F（n）=0；
　　AB垂直于光，在其平面的M内影长|AB1|=AB，F（n）=1；
　　于是有，0=|AB|×0+X
　　则，X=0
　　|AB1|=|AB|×F（n）
　　三、考察三角形ABC，∠A、∠B、∠C的对边边长分别为a、b、c，顶点A、B、C到对边的高分别为AA1、B B 1、CC1，∠A、∠B、∠C在邻边上的造影能力分别为F（A）、F（B）、F（C）。
　　当造影在三角形ABC外部时，允许角造影能力F（A）、F（B）、F（C）取负值。三角形ABC位直角三角形时，允许角造影能力F（A）、F（B）、F（C）取零值。
　　求证：a2+ b2-c2=2ab cos C
　　a2+ c2-b2=2ac cos B
　　b2+ c2- a2=2bc cos A
　　观察（图一）锐角三角形ABC，（图二）钝角三角形ABC（∠B>90°），（图二）直角三角形ABC（∠B=90°）
　　当垂直光平行于高AA1时，则有，
　　a = b×F（C）+ c×F（B）；---------------------①式
　　当垂直光平行于高BB 1时，则有，
　　b = a×F（C）+ c×F（A）；----------------②式
　　当垂直光平行于AB边上的高CC1时，
　　c = b×F（A）+ a×F（B）-----------------③式
　　将①式、②式、③式两边分别同乘以a、b、c，则有
　　a2 = a× b×F（C）+ a×c×F（B） ---------------④式
　　b2 = a×b×F（C）+ b×c×F（A） ---------------⑤式
　　c2 = b×c×F（A）+ a×c×F（B） ---------------⑥式
　　将④式+⑤式-⑥式，消去F（A），F（B），则得：
　　a2+ b2-c2=2ab F（C）
　　同理，可得：
　　a2+ c2-b2=2ac F（B）
　　b2+ c2- a2=2bc F（A）
　　根据角的余弦值定义，并在直角三角形中验证，则有：

　　北极光 2016年4期