黄幼红

　　

　　

　　

　　摘 要：计算不仅贯穿于整个小学数学教学，在日常生活中运用到计算的地方也随处可见。因此，培养学生的运算能力对学生的学习与生活都起着举足轻重的作用。本文从运算含义，在数形结合中生成;算理算法，在数形结合中厘清;运算规律，在数形结合中凸显;算法优化，在数形结合中提升四个方面阐述如何借助数形结合，培养运算能力。

　　关键词：数形结合;运算能力

　　数学运算能力既是数学学科独有的，又与数的运算“直接对应”，是数学学习的关键能力。借助数形结合，有助于帮助儿童形象、直观地理解运算意义和算理的过程中掌握算法，从中寻求合理、简洁的运算方法，实现算法优化，提高运算能力。下面，笔者结合自身课堂教学实际，谈谈在计算教学中借助数形结合，培养运算能力的几点做法，旨在抛砖引玉。

　　一、运算含义，在数形结合中生成

　　运算意义既是学习具体运算的基础，也是解决相关实际问题的依据。儿童能否在头脑中建立准确、深刻的运算意义，必然对其运算能力的发展产生重大影响。教学中如果教师能借助数形结合，以形释义，通过学生具体的操作和直观图式，就可以让一些十分抽象的意义变得形象、直观、简单，让学生清晰地理解运算含义，形成概念。

　　二、算理算法，在数形结合中厘清

　　算理是运算能力的核心成份，它与算法共同构成运算能力的“一体两翼”。算理为算法提供理论依据，是对算法的建构与解释。没有（不讲或不理解）算理的算法是机械的，是不具有迁移性和生长力的。学生只有在理解了算理的基础上才能把机械化的模仿练习变为自主探索算理本质的思维活动。在算理教学中借助数形结合，可以把语言描述难以理解的抽象算理有形的显现出来，使学生真正地理解算理，内化算理。

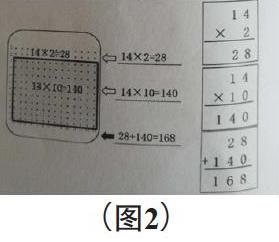
　　例如，在教学《两位数乘两位数的笔算乘法》时，笔者紧扣教材新增的点子图，意图让学生借助点子图将抽象的计算教学直观化、形象化、简单化，努力为学生搭桥铺路，让学生在点子图中明理得法。首先让学生估算“14×12”的结果，有的学生估成“14×10”，有的学生估成“10×10”，有的学生估成“10×12”，接着出示点子图，让学生在点子图上找到估算的部分（如图1），从中明白三种估算方法都是合理的，只是结果都估小了。如果要求实际的本数就应该把没估到的部分加上去。接着让学生试着将自己的想法用算式表示出来，写在横线上，并将相对应的竖式写在右边的方框里。再引导学生思考14×2=28表示什么？14×10=140表示什么？140+28=168又表示什么？然后让学生检查相对应的竖式是否书写正确并让学生尝试将三个竖式综合成一个竖式（如图2）。最后笔者又运用课件教学中色块的呈现帮助学生理解28是怎么来的？140呢？168呢？140的“0”为什么可以不写？（如图3）在此过程中，学生借助图形清晰再现计算过程，清楚的知道每一部分的来龙去脉，这样的形象直观，更易于学生理解算理，明理得法。

　　三、运算规律，在数形结合中凸显

　　在计算教学中，运算规律也是一部分重要的内容。很多学生对运算规律的理解只停留在机械地识记和单纯地模仿层面，他们只经历了从“数”到“数”，从“算”到“算”的建构过程，对运算规律的内涵感悟不深。那么用什么表征才能让学生真正理解运算规律的概念呢？笔者认为借助数形结合将运算规律与图形巧妙融合，可以很好地揭示运算定律的内涵。

　　例如，教学《积的变化规律》时，大部分老师都是先呈现几组乘法算式，让学生观察，比较因数的变化规律，最后得出规律。直观过程从“数”到“数”，虽然能发现规律，但明显感觉不够张力。如果这样来教：先呈现一个长方形（如图4），然后引导学生猜想：当长方形的长不变，宽扩大到原来的4倍时，那么长方形的面积会如何变化？借助课件演示慢慢“变高”的长方形，学生很容易观察到面积也扩大到原来的4倍;当宽不变，长扩大到原来的4倍时，长方形会变得越来越“胖”，面积也扩大到原来的4倍;当长不变时，宽缩小到原来的，长方形就变得越来越“矮”了，直至面积缩小到原来的;当宽不变，长缩小到原来的，长方形就会变得越来越“瘦”，最终面积缩小到原来的。这样通过数形结合，以形思数，让学生经历从具体到抽象，又从抽象到具体的过程，发挥直观对抽象的支柱作用，揭示数和形之间的内在联系，形象的突出了运算定律和运算规律的内涵，还可以让学生从错综复杂的关系中，发现了简单而清晰的关系，使得学生对运算定律和运算规律的记忆和理解更深刻，在计算过程中能灵活应用定律和规律，大大提高了运算能力。

　　四、算法优化，在数形结合中提升

　　在计算教学中，有时我们会碰到一些特别的数学算式，如果按部就班的计算，过程会相当复杂繁琐，可如果借助直观图形，以“形”的手段将算式形象化，让学生看到图联想到算式，看到算式联想到图，通过直观图形的特点，把计算中问题的本质直观的表达出来，不仅可以避开繁琐的运算，突破计算的难点，优化了算法，让计算变得更加简单，大大提高学生的计算能力和计算速度，也提升了学生的思维深度，从而将数形结合思想深植于脑中。

　　例如，教学“+++++++……”时，大部分的学生一开始都会想通分，可是这道题由于加数个数是无限的，如果采用先通分再计算的话，工程量很大，既耗时又费力，要想正确计算出最后的结果难度系数很大。此时，如果我们引导学生先仔细观察算式特点，再通过图形，把这些加数分别在图形上表示出来（如图5），在边分边画的过程中，学生自然而然能够从中感悟到如果再无限的加下去的话，就是一整个圆形，也就是1。也就说明这些分数不断加下去，总和就是1。这样借助图形，另辟蹊径，不仅计算过程简单快捷，解决起來直观明了，而且大大提高了学生数学的理解能力，提升了学生的运算能力。

　　综上所述，借助数形结合，培养运算能力，应当以明晰“运算含义”为基础，以理解“算理算法”为核心，以掌握“定律规律”为主线，以“优化算法”为目标。教学中，有效借助直观图形，时时做到“借形思数”、“数形结合”才能让数形结合的思想在学生的脑中生根发芽，从而优化计算教学，提高学生的运算能力，让学生做到“神机妙算”。

　　参考文献：

　　[1]王珍.“简约智慧”数学教学[M].福建教育出版社.2014.12.