于川东 乌鲁木齐市第七十中学 新疆乌鲁木齐 830011

　　2018年，新疆乌鲁木齐市教研中心举行举行了一次初中说题比赛，参赛教师根据比赛提供的历年乌鲁木齐市数学中考的压轴题,需要按照“解法分析—题目立意—功能和价值—预测试题”的步骤撰写课件.现结合说题比赛过程中的案例，谈谈自己参加这次比赛的一些思考.

一、试题的呈现

（1）求点C的坐标；

　　（2）设直线y＝2x与抛物线交于A，B两点（点A在点B的左侧）：

　　在抛物线的对称轴上是否存在点G，使∠AGC＝∠BGC？若存在，求出点G的坐标；若不存在，请说明理由；

　　（3）点P在直线y＝2x上，点Q在抛物线上，当以点O，M，P，Q为顶点的四边形是平行四边形时，求点Q的坐标.

　　

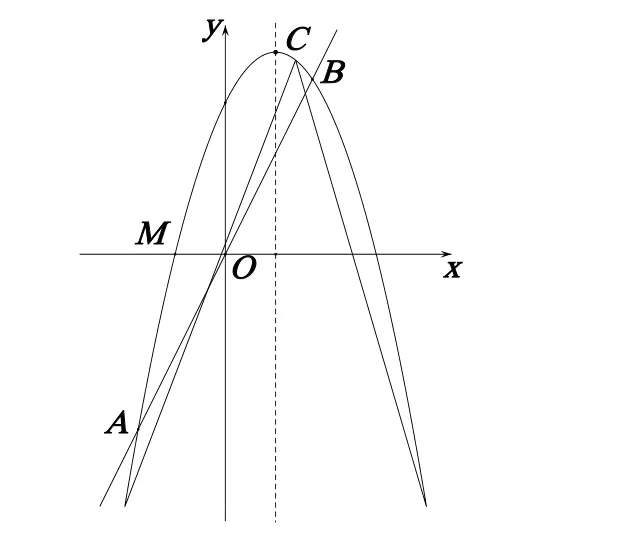
　　图一

二、试题的解法分析

解：（1）由题意得－ 1－2 ＋ n＝ 0，解得 n＝3， 得 C（1,4）

　　（2）存在符合条件的点G.

　　（方法1）求得交点A、B 坐标，再做点B关于对称轴的对称点B’,连接AB’交对称轴于点G，连接BG，则∠AGC＝∠BGC，设直线AB’解析式y=kx+b，解直线AB’解析式，最后得 G（1，6）

　　（方法2）过A、B两点作对称轴x=1的垂线AP和BQ，设G（1，a），

　　∵∠AGC=∠BGC，∠APG=∠BQG=90°，

　　解得a=6,得G（1，6）

　　【点评】这一问运用几何画板动态演示并度量出两个角度的大小，能直观的表达讲解意图.

　　（3）设 P（m，2m）

　　①当四边形OMQP是平行四边形时，

　　则 Q（m-1，2m），

　　∴ 2m=-（m-1）2+2（m-1）+3，

　　解得：m=0或2，

　　∴ Q1（-1，0）（舍），Q2（1，4），

　　②当四边形OMPQ是平行四边形，

　　③当OM是对角线时，分别过P、Q作x轴的垂线，垂足分别为G、H，可得△PGM≌△QHO，

　　∴ Q5（-1，0）（舍），Q6（1，4），

　　【点评】如果借助几何画板动态演示平行四边形产生的过程，可以得到更富有启发性的讲解效果,提高解题效果.

三、题目立意和其他变式

第⑴问属于基础性的考查,来自九上二次函数第56页第4题第（1）小题的变形.

　　第（2）问考查了化归思想、数形结合思想、方程的思想。还可以进行以下变式：将问题∠AGC＝∠BGC改为当△AGM周长最小时，求点G.

　　第（3）问考察平行四边形存在问题，考查了分类讨论、数形结合、方程与函数、化归等思想.

四、本题功能和价值

试题突出考查了函数思想在几何中的运用，涵盖了方程、函数、平行四边形等知识.试题在考查学生运算能力以及思维的灵活性、广阔性方面具有较高的效度.

五、预测此类试题的趋势和方向

1.基础性：一定要注意核心概念、基础知识，不脱离基础.

　　2.综合性：指代数、几何等内容的基础知识、基本思想方法的自然融合和联系.

　　3.启发性：对学生思维的启发，能激发学生思维的创造力.

　　4.难度适中：不能任意的拔高难度.

　　说题比赛对于参赛教师各方面的能力要求很高.首先就解题能力而言，说题比赛要求提供尽可能多的解法和变式；其次说题比赛考察的是选手从多角度阐述一道试题的能力，这一点对教师的专业成长有极大的帮助；最后，说题比赛更关注参赛教师如何站在中考出题者的角度考虑试题的趋势和方向，因此是一种更贴近教学实际的教研活动.