李梦辰

　　(重庆交通大学 经济与管理学院，重庆 400074)

1 利用AHP法对股票投资组合选择

1.1 建立递阶层次结构模型

充分分析股票信息相关的知识后，依据层次分析法的基本思想如下:

　　第一层:目标层。目标层是最高层，是决策问题的目标，本文即为“选择股票”，本层由A代替。

　　第二层:准则层。包括实现目标的中间环节，根据引言中的分析，本次决策过程中的具体元素为主观因素B、客观因素B和宏观因素B。

　　第三层:子准则层。根据分析，子准则元素具体为心里预期C、风险偏好C、人为操控C、公司运营C、股价C、市场利率C、行业情况C、通货膨胀C、政治因素C、经济政策C。

　　由此构造的股票层次结构，如图1。

1.2 构造判断矩阵

假定某一层次的元素B作为准则，对下一层元素有支配作用；我们在准则B下，根据下一层各元素之间两两的相对重要性赋予各元素一定权重数值。于是我们可以得到一个判断矩阵C=(C)，也就是说C是权重值，表示因素i和因素j相对于准则B的重要值。判断矩阵的一般形式如下:

　　在此原理基础上，对于股票选择模型，根据股票行业分析，我们可以得到以下矩阵:

　　

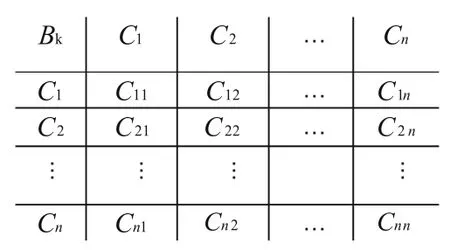
　　(1)准则层对目标层的判断矩阵A-B(简记为A):

　　

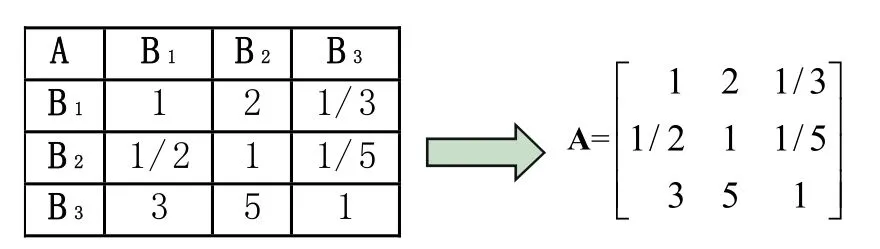
　　(2)同理，子准则层对准则层的判断矩阵B、B、B为:

　　

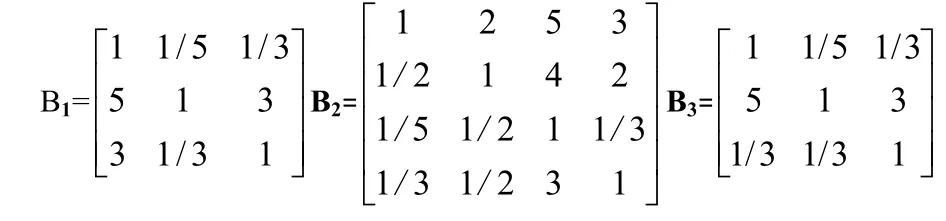
1.3 层次单排序和判断矩阵一致性检验

建立判断矩阵是为了计算单层次排序问题。然而在实际中，衡量两元素的相对重要性时，各专家给的意见，会出现矛盾的情况，为避免评价结果失真，我们在计算权重的同时需要对判断矩阵进行一致性检验。

　　根据理论计算公式，

　　

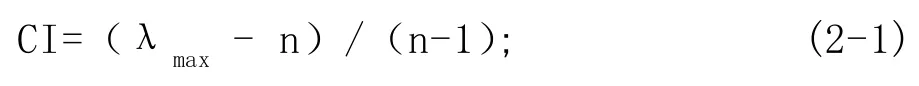
　　平均随机一致性指标:

　　

　　如果CR＜0.1，我们就认为判断矩阵通过了一致性检验，否则需调整Cij的值，使其通过一致性检验。

　　

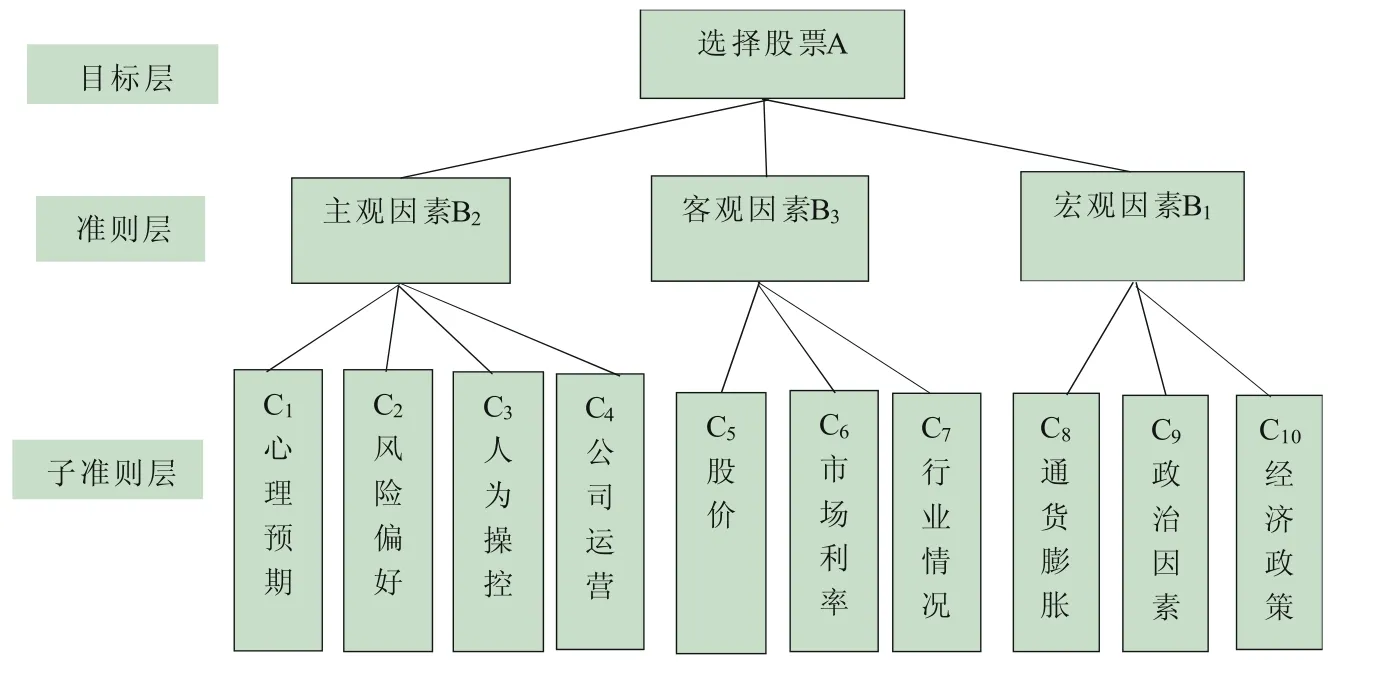
　　图1 股票选择需考虑的因素层次结构图

　　求解单层次排序的权向量时，我们采取方根法。

　　在本例中，权向量的求解及一致性检验的计算结果，如表1。

　　

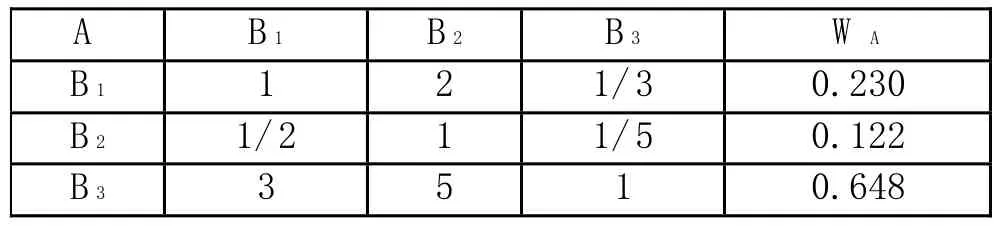
　　表1-1 判断矩阵A-B的单层次排序

　　

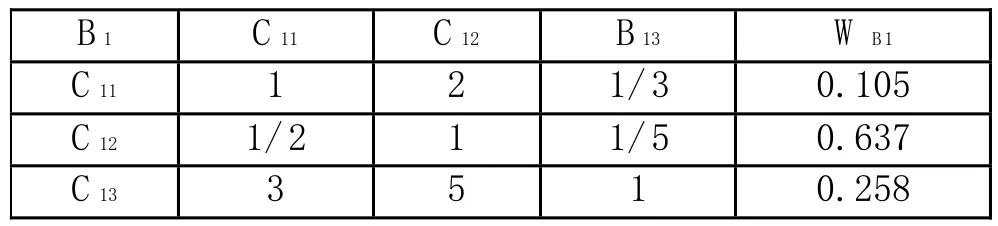
　　表1-2 判断矩阵B1-C的单层次排序

　　

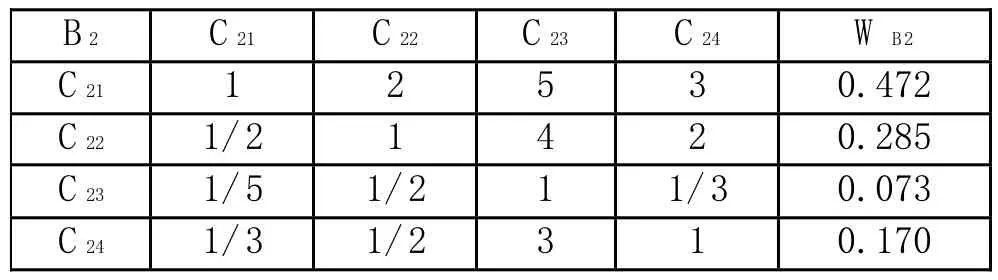
　　表1-3 判断矩阵B2-C的单层次排序

　　

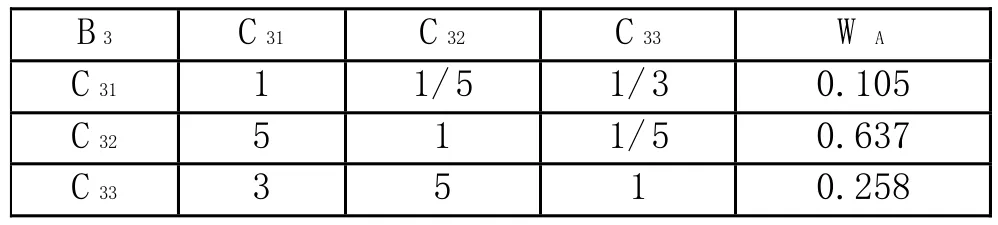
　　表1-4 判断矩阵B3-C的单层次排序

1.4 层次总排序

因此，需要计算各层元素对系统目标的合成权重，进行总排序，以确定结构图中最底层各个元素在总目标中的重要程度。这一过程是最高层次到最低层次逐层进行的。层次总排序的计算结果，如表2。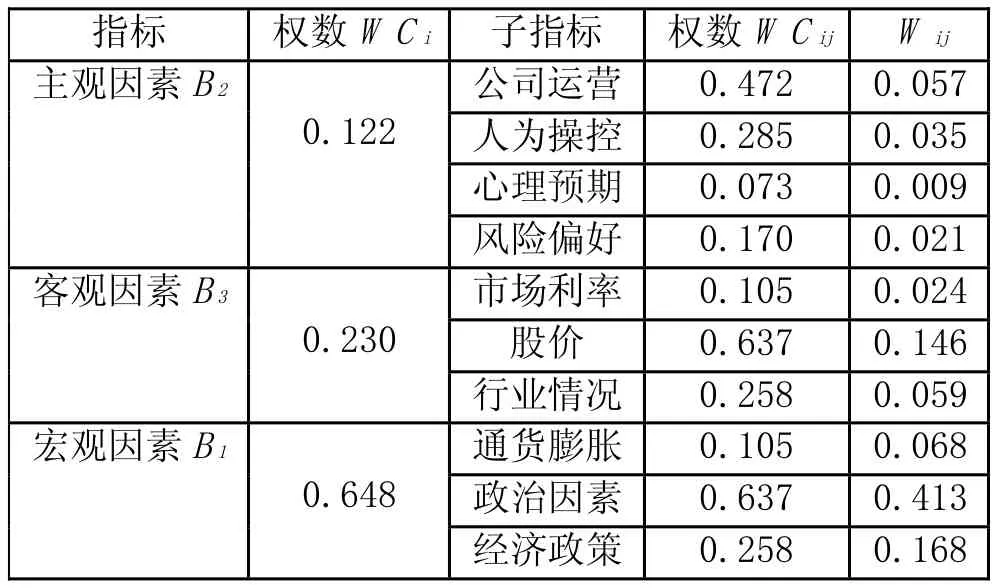

　　

　　表2 股票选择需考虑因素的层次总排序

1.5 股票投资组合选择

对于股票投资者来说，在选择股票时，可以利用层次分析法对股票选择考虑的因素进行权重分析后，再根据行情数据来对各要素打分，通过对权重和得分的加权计算方法来对股票进行组合选择，如表3。

　　1.5.1 单支股票计算

　　对三支股票:唯品会、王府井、深高速，给出得分，如表4。

　　加权后的总得分为:

　　(1)唯品会:

　　

　　(2)王府井:

　　

　　

　　表3 平均随机一致性指标(RI值)

　　

　　表4 三支股票的得分情况

　　(3)深高速:

　　

　　1.5.2 股票组合选优

　　马科维茨在其文章中研究的股票投资组合原理就在此，其中验证了证券投资市场中的古话:“不要把所有的鸡蛋都放到一个篮子里”。

　　根据上述股票计算的数据，根据股票组合的比例和单只股票的总得分进行加权计算后。我们可以将股票组合为以下几种情况:

　　单支股票类型:A，B，C；股票组合类型:AB，AC，BC，ABC，如表5。

　　

　　表5 股票投资组合选择

2 结语

根据以上计算结果，我们可以发现，单支股票的得分排序为:S＞S＞S；股票组合的得分排序为:S＞S＞S＞S；即单只股票投资应选唯品会，股票组合投资就应该选择唯品会和深高速的组合(一个处于行业的上升发展期，另一个在行业中一直较为稳定，这样组合的风险最小)。本文对于股票投资组合的论证可以总结为:(1)对于处于行业中发展势头好的行业，投资盈利性高，因此相比股票的稳定性更在乎收益的投资者可以选择此类股票单独投资；(2)对于股票组合投资来说，选择一支收益高且稳定的股票是最理智的投资选择，既能规避风险，而且能获得可观的收益(如组合AC)；(3)在选择股票组合时，比例的确定可以采取的方法:收益高＞稳定性好＞收益低；

　　当然，本次对于股票组合的选择研究只是基于层次分析法确定的各个影响因素的权重，对于各因素的得分是根据行情分析，组合比例的确定偏主观，选优结果不够完善；所以，在不同的行情下，需要更加科学的组合比例确定原则进行分析选择最优组合。