
摘 要:信息化时代数学课程资源的有效整合,对数学教学意义重大,对教学方式和学习方式的变革有很大的促进作用,对于培养学生的核心素养,引导学生形成数学思想方法及正确的价值观有现实而深远的影响。本文主要就课堂教学中生成性资源的收集和利用进行总结,以案例形式进行说明,并且结合教学实际,说明生成性课程资源的形成及利用。
关键词:课程资源;生成性资源;利用方式
信息化时代数学课程资源的有效整合,对数学教学意义重大,对教学方式和学习方式的变革有很大的促进作用,对于培养学生的核心素养,引导学生形成数学思想方法及正确的价值观有现实而深远的影响。数学课程资源是指应用于教与学活动中的各种资源。主要分为以下几类:①文本资源主要包括文本资源——如教科书、教师用书,教与学的辅助用书、教学挂图等;②信息技术资源——如网络、数学软件、多媒体光盘等;③社会教育资源——如教育与学科专家,图书馆、少年宫、博物馆,报纸杂志、电视广播等;④环境与工具——如日常生活环境中的数学信息,用于操作的学具或教具,数学实验室等;⑤生成性资源——如教学活动中学生提出的问题等。
本文主要就课堂教学中生成性资源的收集和利用进行总结。生成性资源主要指教学活动中教师或学生提出的问题、学生的作品、学生学习过程中出现的问题等。下面以案例形式进行说明,并且结合教学实际,说明生成性课程资源如何利用。
案例一:复习课中的生成性资源及利用
活动1:完成以下练习
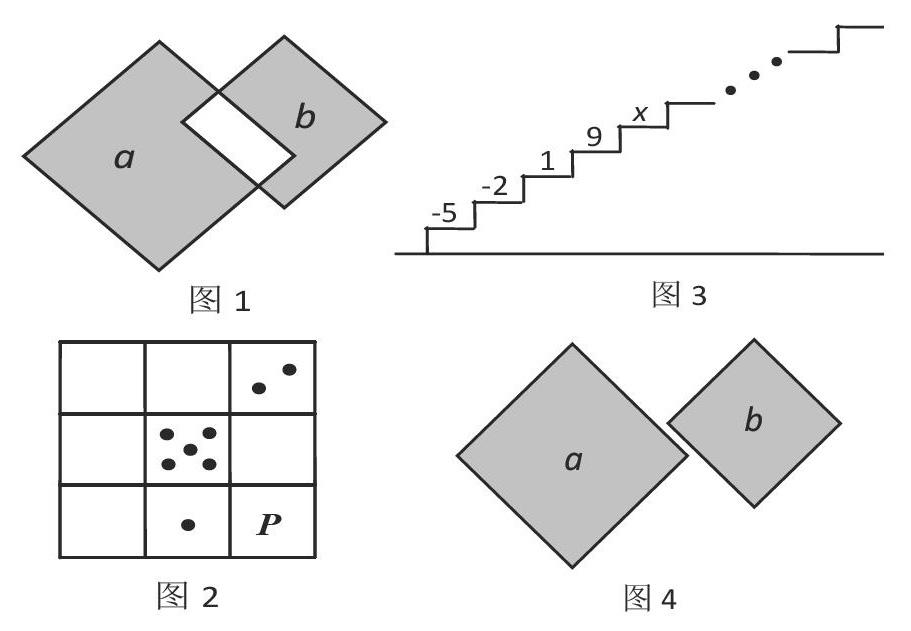
1.(2012年河北卷11题)如图1,两个正方形的面积分别为16,9,两阴影部分的面积分别为α,b,则α-b等于( )
A.7 B.6 C.5 D.4
2.(2007年河北卷8题)我国古代的“河图”是由3×3的方格构成,每个方格内均有数目不同的点图,每一行、每一列以及每一条对角线上的三个点图的点数之和均相等.图2给出了“河图”的部分点图,请你推算出P处所对应的点图是(? ? )
A? ? ? ? ? ?B? ? ? ? ? C? ? ? ? ?D
3.(2018年河北卷20题)如图3,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着﹣5,﹣2,1,9,且任意相邻四个台阶上数的和都相等。
尝试(1)求前4个台阶上数的和是多少?
(2)求第5个台阶上的数是多少?
应用 求从下到上前31个台阶上数的和.
发现 试用k(k为正整数)的式子表示出数“1”所在的台阶数.
活动2:在解决以上练习的过程中,请对各题的解法进行比较分析。
我们以例1为例进行分析,例1 中通过图形展现了两个正方形的位置,而公共部分(即图中的空白部分)如何表示是解决问题的关键。这是2012年河北卷11题,学生的解法可谓多种多样,比如有的同学由两个正方形的面积分别为16,9,求出两个正方形的边长分别为4,3,两阴影部分的面积与空白部分的面积有何关系?看不出来,解题思路会受阻;但是有的同学会有不同的方法,现总结如下:
解法一(列代数式法):设公共部分的面积为χ,
则α=16-χ,b=9-χ,∴α-b=7。
解法二(方程思想):由题意知,16-α=9-b,
等式两边是公共部分不同表示方法,整理得:α-b=7。
解法三(方程思想):16-α+b=9(或9-b+α=16),方程左边表示的是小(或大)正方形面积,整理得:α-b=7。
解法四(整式计算):
α-b=(α+χ)-(b+χ)=16-9=7。
解法五(特殊位置法):如圖4,则α-b=16-9=7
解法六(特值法):
令χ=1,则α=15,b=8,∴α-b=7
首先直观感知,再通过计算验证,体现了代数中的合情推理到推断的思维过程,各种解法蕴含了方程和化归思想。好的问题情境,科学的呈现方式,不但能给学生提供直接的信息,还可能隐藏着一些有用的信息。在复习课中,我们把以上看似无关的题目放在一起,
我们研究中考试题,把中考题当做一种课程资源,经过了深入思考,对题目潜在的价值进行了挖掘,把看似不相干的题目放在一起。学生在解题过程中,自己就能感受到数学思想方法的力量。这些题有什么共同点?这些隐含的信息起到怎样关键的作用?这样复习课中就很容易产生生成性资源——学生的不同解法,我们将这些生成性资源在课堂上加以利用,以一题多解的形式,引导学生感悟数学思想方法的运用,在对多种解法的比较分析中,逐渐接近数学本质。所以,在教学过程中恰当的使用数学课程资源,在很大程度上提高了学生从事数学活动的水平,那么学生就会喜欢上复习课,乐学也会学,在数学课上学有所获,数学素养在潜移默化中逐渐提高。
案例二:数学活动中的生成性资源及利用
《矩形的折叠》教学设计片段
【教材分析】本节课是《义务教育课程标准实验教科书·数学》(人教版)八年级下册第十八章章末的数学活动,是在学习了平行四边形整章知识之后,围绕特殊四边形展开的一节活动课。其教学内容为:让学生动手操作经历矩形折叠的过程,探索折叠后线段的关系;用矩形折出特殊的30°角,体验折叠方法的多样性。本节课不但需要综合运用轴对称,矩形性质,等边三角形的相关知识,而且用到了分类讨论,方程思想,转化思想,为今后解决探究类问题提供了思路和方法。
【教学过程】
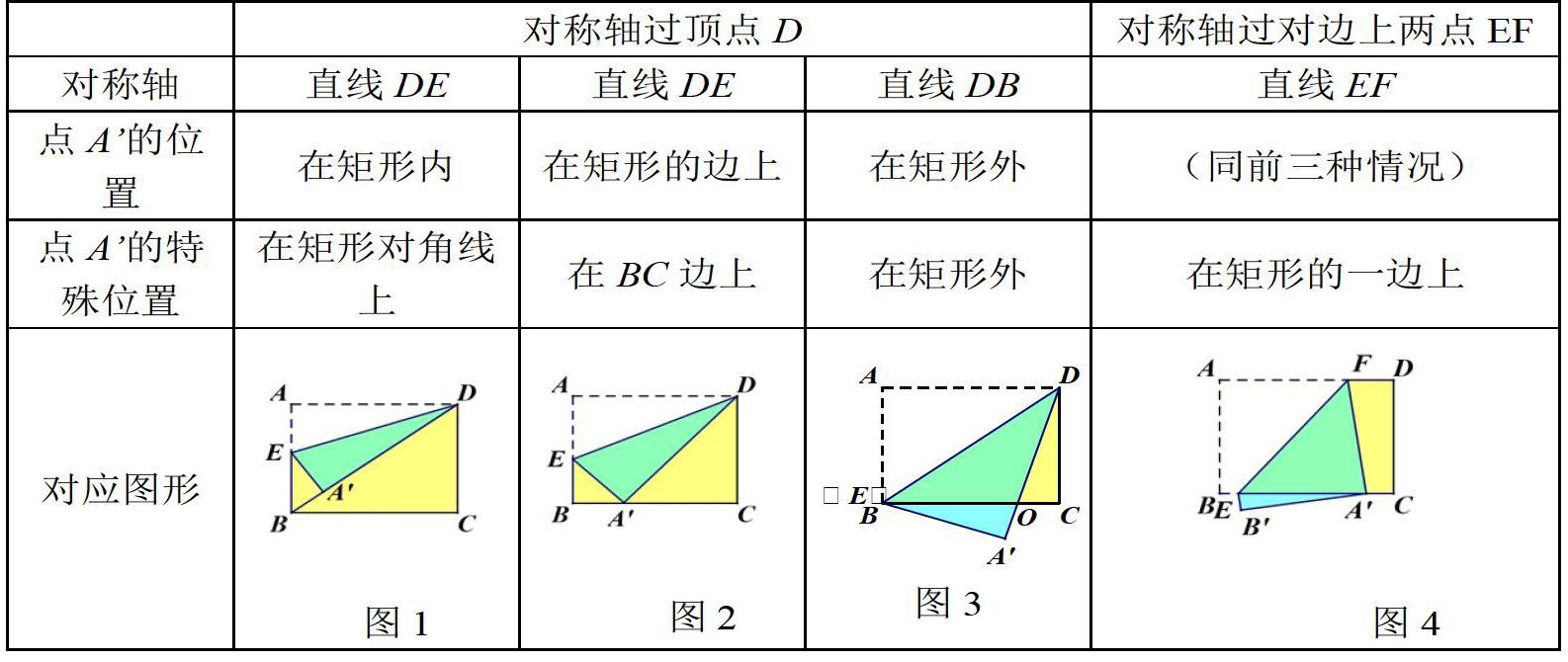
动手操作:请同学们准备一张矩形纸片ABCD,按以下要求进行折叠:(1)将矩形沿过点D的直线折叠,观察点A折叠后的位置A,你能找到点A的哪些特殊位置?(2)若对称轴是过AD,BC上任意两点E,F的一条直线,将矩形折叠,点A折叠后的位置为A,你能找到点A哪些特殊位置?请你画出相应的图形。
展示归纳:学生画图展示,教师几何画板演示并总结
我们研究特殊位置,会出现一些有趣的几何图形,也能计算相应的线段长。老师给出第1题:如图1,若AB=6,AD=8,则AE=? ? ? ;还能求出哪些线段长?
同学们,你们自己也能出一些题吗?来试试吧。
(学生给出如下问题)
2.如图2,若AB=6,AD=10,求AE;
3.如图3,求证:重叠部分的三角形是等腰三角形;
4.如图4,连接AE,判断四边形AFAE的形状,并说明理由。
......
这些问题的设计、呈现及解决,是我们课堂教学中宝贵的生成性资源。以往,学生对折叠类问题的掌握就是多做题,靠题海战术,无形中增加了学习负担。但是,在数学活动课上,学生对于折叠类的问题,能自主编制试题,能自己解决问题,他们悟出了学习数学的方法,真正感受到数学学习的乐趣,激发了学习数学的兴趣。
案例三:利用网络教研促进生成性资源的推广
我们课题组的吴义红老师在进行中考复习时,有一节函数复习课的设计非常有特点,上课效果非常好。这是她在复习课教学中的生成性资源,我们利用现代化信息技术手段,面向全市教师开展了一次网络教研。
《中考总复习函数专题》教学设计片段
片段一:
由一道题引发的思考:(2015河北23题)水平放置的容器内原有210毫米高的水,如图.将若干个球逐一放入该容器中,每放入一个大球水面就上升4毫米,每放入一个小球水面就上升3毫米,假定放入容器中的所有球完全浸没水中且水不溢出.设水面高为y毫米.
(1)只放入大球,且个数为x大,求y与x大的函数关系式(不必寫出x大的范围);
(2)仅放入6个大球后,开始放入小球,且小球个数为x小.
①求y与x小的函数关系式(不必写出x小的范围);
②限定水面高不超过260毫米,最多能放入几个小球?
吴老师通过学生熟悉的一道中考题,让学生感知解决问题需要的最基本知识本质是什么?从而引出本节课甚至是接下来的几节课我们需要研究的最本质的数学知识是什么。
活动一:什么是函数?从课本到生活,从教师到学生,从现象到本质。师生合作探究了函数定义的本质。
(1)(人教版八年级下册P73)图19.1-2是体检时的心电图,其中图上点的横坐标x表示时间,纵坐标y表示心脏部位的生物电流,它们是两个变量.在心电图中,对于 X的每一个确定的值,y都有唯一确定的值与其对应吗?
(2)(人教版八年级下册P74)(4)水池中有水10L,此后每小时漏水0.05L,写出水池中的水量V(单位L)随时间t(单位h)变化而变化。




