刘清扬 河北省衡水市郑口中学 河北省 衡水市 253000

　　离心率是描述圆锥曲线形状特征的一个重要概念，是椭圆、双曲线、抛物线三类二次曲线的统一定义的桥梁和纽带.离心率问题内涵丰富且综合性强，是各级训练测试及高考中的热点之一.下面结合实例，分析求解圆锥曲线离心率的常用的“策略”.

　　策略一 借助公式、定义

　　根据圆锥曲线的标准方程或a、b、c对应的值，直接利用离心率公式来求解离心率的问题，关键在于求圆锥曲线的标准方程或a、b、c对应的值.

　　

　　策略二 借助方程

　　根据题设条件，借助a、b、c之间的关系，求出关于a、c的方程关系式，进而得到关于离心率e的方程，从而通过解方程来得到离心率e，关键是构造相应的方程，但解方程时要注意对应圆锥曲线的离心率的特征.

　　

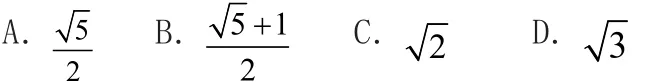
　　策略三 借助统一定义

　　由圆锥曲线的统一定义知，圆锥曲线的离心率e是平面上动点到焦点的距离和动点到准线的距离之比，特别适用于条件含有焦半径的圆锥曲线问题及其他相关问题。关键是抓住圆锥曲线的统一定义，结合题意求解.

　　

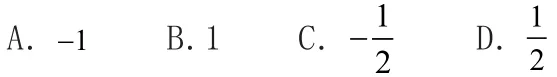
　　策略四：借助平面几何知识，或圆锥曲线上点坐标的范围

　　根据题设中的条件建立a、b、c之间的不等式关系，进而得到关于离心率e的不等式，通过求解不等式来求离心率的范围，关键是构造相应的不等式，但解不等式时要注意对应圆锥曲线的离心率的特征.