我们知道,机械能守恒定律是指在只有重力或弹力对物体做功的条件下(或者不受其他外力的作用下),物体的动能和势能(包括重力势能和弹性势能)发生相互转化,但机械能的总量保持不变。对于机械能守恒的理解,我们要注意如下三种情况:①只受重力作用,如在不考虑空气阻力的情况下的各种抛体运动,物体的机械能守恒;②受其他力,但其他力不做功,只有重力或系统内的弹力做功;③系统内的弹力做功伴随着弹性势能的变化,并且系统内弹力做功等于系统弹性势能的减少量。
一、准确理解机械能守恒定律
对于机械能是否守恒的判断方法有三种:①直接判断:机械能包括动能、重力势能和弹性势能,判断机械能是否守恒可以看物体或系统机械能的总和是否变化;②从做功的角度判断:若物体或系统只有重力或系统内弹力做功,虽受其他力,但其他力不做功,机械能守恒,诸如绳子突然绷紧,物体间非弹性碰撞等,机械能均不守恒;③从能量转化的角度来判断:若物体系统中只有动能和势能的相互转化而无机械能与其他形式的能的转化,则物体系统机械能守恒。而机械能守恒定律的表达形式有许多,经常涉及的有下列三种形式:
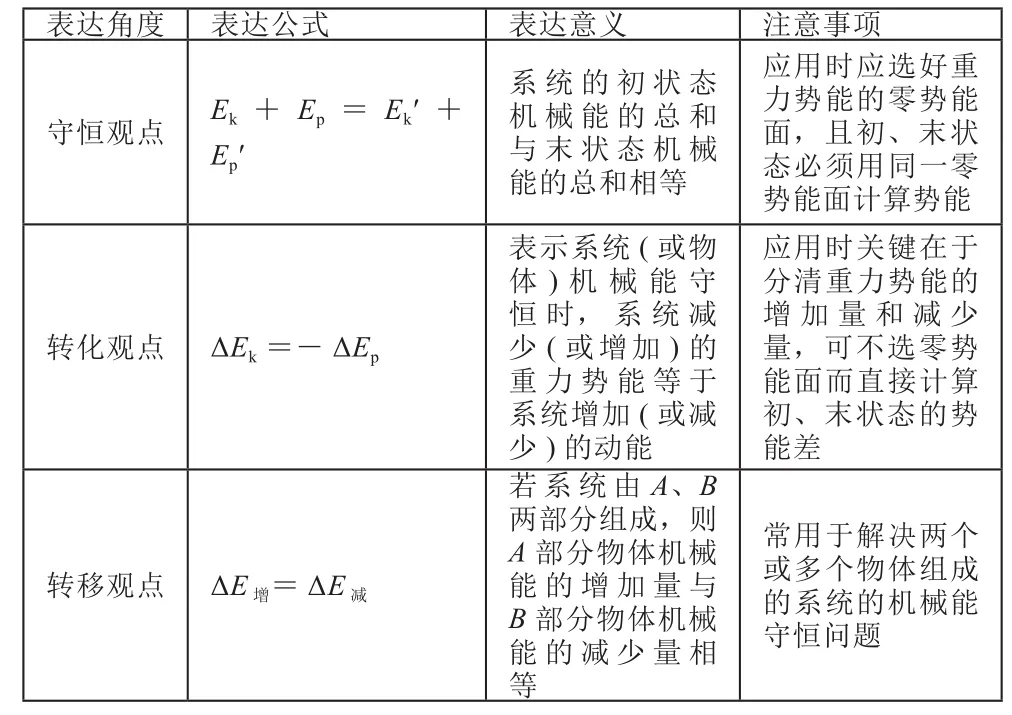
表达角度 表达公式 表达意义 注意事项守恒观点 Ek+ Ep= Ek′+Ep′系统的初状态机械能的总和与末状态机械能的总和相等应用时应选好重力势能的零势能面,且初、末状态必须用同一零势能面计算势能转化观点 ΔEk=-ΔEp表示系统(或物体)机械能守恒时,系统减少(或增加)的重力势能等于系统增加(或减少)的动能应用时关键在于分清重力势能的增加量和减少量,可不选零势能面而直接计算初、末状态的势能差转移观点 ΔE增=ΔE减常用于解决两个或多个物体组成的系统的机械能守恒问题若系统由A、B两部分组成,则A部分物体机械能的增加量与B部分物体机械能的减少量相等
单物体多过程机械能守恒问题:划分物体运动阶段,研究每个阶段中的运动性质,判断机械能是否守恒。
对于多物体组成的系统的机械能守恒,一般选用ΔEp=-ΔEk或者ΔE增=ΔE减形式,优势在于不用选择零势能面。解题时,需要找到两物体的速度关系确定系统动能的变化,同时找到两物体上升或下降的高度关系确定系统重力势能的变化,再按照系统动能的变化等于重力势能的变化列方程求解。此类问题中,寻找两物体的速度关系、高度变化情况以及机械能的转化情况是求解问题的关键。
二、利用机械能守恒定律解决物理问题
1、单个物体的机械能守恒
【例1】在一斜面顶端,将甲乙两个小球分别以v和v/2的速度沿同一方向水平抛出,两球都落在该斜面上。甲球落至斜面时的速率是乙球落至斜面时速率的 ( )A. 2倍 B. 4倍 C. 6倍 D. 8倍
【解析】此题将平抛运动、斜面模型、机械能守恒定律有机融合,综合性强。对于小球在斜面上的平抛运动,一般利用平抛运动规律和几何关系列方程解答。
设甲球落至斜面时的速率为v1,由平抛运动规律,,设斜面倾角为θ,由几何关系,得小球抛出到落在斜面上机械能守恒,则,联立以上各式得同理乙球落至斜面时的速率因此本题正确答案为A。
2、系统的机械能守恒
【例2】如图所示,钉子A、B相距5l,处于同一高度.细线的一端系有质量为M的小物块,另一端绕过A固定于B.质量为m的小球固定在细线上C点,B、C间的线长为3l。用手竖直向下拉住小球,使小球和物块都静止,此时BC与水平方向的夹角为53°。松手后,小球运动到与A、B相同高度时的速度恰好为零,然后向下运动。忽略一切摩擦,重力加速度为g。求小球向下运动到最低点时,物块M所受的拉力大小T。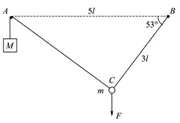
【解析】根据机械能守恒定律,小球向下运动到最低点即为小球的起始点。显然,此时AC垂直于BC。设此时AC方向的加速度大小为a,重物受到的拉力为T,小球受AC的拉力T′=T
对小物块M,根据牛顿运动定律,有 Mg–T=Ma
对小球m,根据牛顿运动定律,有 T′–mgcos53°=ma解得
3、多个物体的连接体问题
【例3】质量均为m的小物体A和B分别系在一根不计质量的细绳两端,绳子跨过固定在倾角θ=30°的斜面顶端的定滑轮上,且斜面固定在水平地面上。开始时把物体B拉到斜面底端,绳与斜面平行,这时物体A离地面的高度为1.8m,如图所示,若不计一切摩擦,从静止开始放手让它们运动,g取10m/s2,求物体A着地时的速度。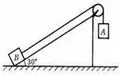
【解析】物体A着地之前,AB组成的系统机械能守恒,设A落地时的速度为v,系统动能的增加量等于系统重力势能的减少量,则得
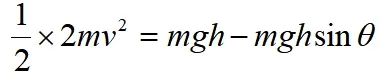
代入数据得:v=3m/s
机械能守恒定律作为物理学的核心知识,是每年高考必须涉及的内容,即可能是选择题,也可能是计算题,甚至也可能以实验题的形式出现,对此,我们必须引起足够的重视。





